搜到的题解我一直读不懂…断断续续做了几天之后决定自己写一篇。
首先,有一个暴力的做法:先固定三角形最左最上方的点,然后依次枚举另外两个点,枚举时保证三点不共线。
这是一个![]() 的做法。显然会
的做法。显然会![]() 。
。
尝试用组合计数的知识解决这个问题:用组合数算出选三个不同点的方案数![]() ,三点在同一行或同一列的方案数
,三点在同一行或同一列的方案数![]() ,三点在同一斜线上的方案数
,三点在同一斜线上的方案数![]() 。答案就是
。答案就是![]() 。
。
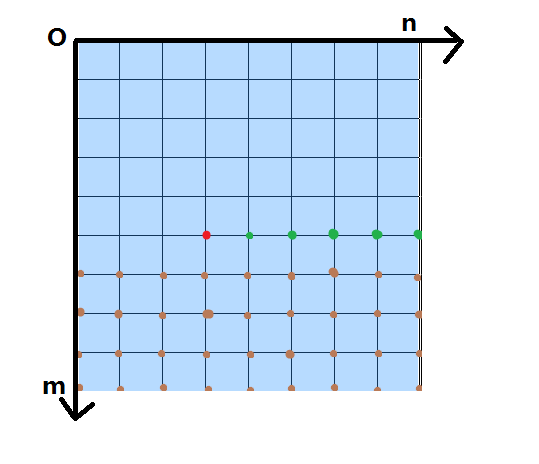
后面的内容将会按照如图所示的坐标系来描述。请先尝试适应这种坐标系表示方法(横纵坐标的方向,![]() 的意义)。(我知道图太丑)
的意义)。(我知道图太丑)
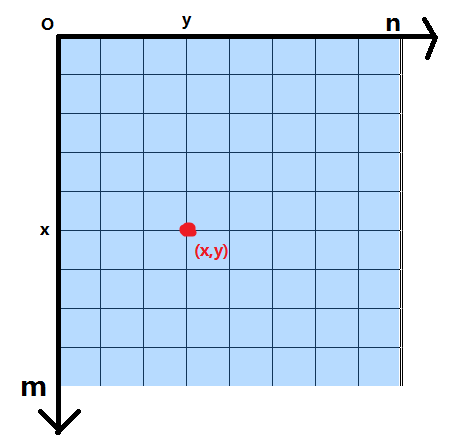
注意![]() 只是格子的数量。可选的点一共有
只是格子的数量。可选的点一共有![]() 个。
个。
计算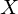 :
:
显然![]() 是在
是在![]() 个元素中任选
个元素中任选![]() 个的组合数,即
个的组合数,即![]()
计算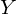 :
:
每行都有![]() 种方案在同一行共线,每列都有
种方案在同一行共线,每列都有![]() 种方案在同一列共线。
种方案在同一列共线。
因此![]()
虽然今天不是愚人节(至少我写这个的时候不是),但是在继续下去算![]() 之前,我们再讨论另外一种直接计算
之前,我们再讨论另外一种直接计算![]() 的方案。这是我第一次写这道题时用的计算方法。(其实把上面的
的方案。这是我第一次写这道题时用的计算方法。(其实把上面的![]() 化简也能得到下面的结果,但我只是提供多一种思路吧…)
化简也能得到下面的结果,但我只是提供多一种思路吧…)
当然,如果你已经因为做这道题搞得头昏脑涨,然后再来看这篇题解,那就可以跳过这部分,先看如何算![]() 。
。
受前面暴力做法的启发(但并不完全和它相同),我们可以发现![]() 就等于
就等于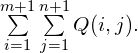 其中
其中![]() 表示以
表示以![]() 为最上最左的顶点,且三点不在同一行或者同一列共线(可能在同一条斜线上共线)的方案数。
为最上最左的顶点,且三点不在同一行或者同一列共线(可能在同一条斜线上共线)的方案数。
为了方便叙述,我们在这里设![]() 。因此共有
。因此共有![]() 个点可以作为三角形的顶点。
个点可以作为三角形的顶点。
考虑如何计算![]() ,设
,设![]() 的坐标为
的坐标为![]() ,另外两个点为
,另外两个点为![]() ,显然有这样几种情况:
,显然有这样几种情况:
1.![]() 与
与![]() 在同一行上,
在同一行上,![]() 在它们的下方。如下图所示。红点为
在它们的下方。如下图所示。红点为![]() ,
, ![]() 可以在所有的绿点中选择(有
可以在所有的绿点中选择(有![]() 个),
个),![]() 可以在所有的棕点中选择(有
可以在所有的棕点中选择(有![]() )个。共有
)个。共有![]() 种方案。
种方案。
可能你会问,如果是![]() 与
与![]() 在同一行,
在同一行,![]() 在它们的下面呢?需不需要把这个方案数乘以
在它们的下面呢?需不需要把这个方案数乘以![]() ?
?
不需要。因为我们计算的是选点的方案数。这里的![]() 指代的是其中的一个点,
指代的是其中的一个点,![]() 指代的是另外一个点。它们的方案数与排列无关。选择的顶点情况一样就应该被认作是同一种方法。
指代的是另外一个点。它们的方案数与排列无关。选择的顶点情况一样就应该被认作是同一种方法。
2.![]() 在
在![]() 的正下方,
的正下方,![]() 在
在![]() 的斜下方。
的斜下方。
为什么![]() 不能与
不能与![]() 在同一行呢?因为这样会和第一种情况有重复。
在同一行呢?因为这样会和第一种情况有重复。
这样![]() 有
有![]() 种选法,
种选法,![]() 有
有![]() 种选法。
种选法。
共有![]() 种选法
种选法
3.![]() 都在
都在![]() 斜下方。
斜下方。
![]() 有
有![]() 种选法,
种选法,![]() 有
有![]() 种选法。
种选法。
共有![]() 种选法。注意要除以
种选法。注意要除以![]() ,因为同一种搭配算了两次。
,因为同一种搭配算了两次。
这就是![]() 的算法了。时间复杂度为
的算法了。时间复杂度为![]() 。它很优秀,可惜极限情况下还是会
。它很优秀,可惜极限情况下还是会![]() 。
。
在上面的讨论里,我们发现:
![Rendered by QuickLaTeX.com Q(i,j)=n'(n'-j)(m'-i)+(n'-1)(m'-i)^2+\frac{1}{2}(m'-i)(n'-1)[(m'-i)(n'-1)-1].](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-46d6eff3c85ba88a45a3023da4b79f16_l3.png)
最后的答案就是:
![Rendered by QuickLaTeX.com \begin{aligned} X-Y&=\sum\limits_{i=1}^{m'} \sum\limits_{j=1}^{n'}Q(i,j) \&=\sum\limits_{i=1}^{m'} \sum\limits_{j=1}^{n'}{n'(n'-j)(m'-i)+(n'-1)(m'-i)^2+\frac{1}{2}(m'-i)(n'-1)[(m'-i)(n'-1)-1] } \end{aligned}](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-bf189137ae92b19a1b8ac12c737bf07e_l3.png)
不急,我们一部分一部分搞定。
设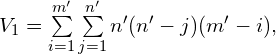
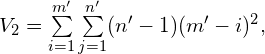
![Rendered by QuickLaTeX.com V_3=\sum\limits_{i=1}^{m'} \sum\limits_{j=1}^{n'} \frac{1}{2}(m'-i)(n'-1)[(m'-i)(n'-1)-1],](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-932ce5fb5f5140d59956f7fde90e20d8_l3.png)
则![]()
先化简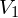 :
:
![]()
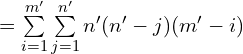
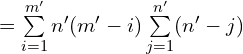
![Rendered by QuickLaTeX.com =\sum\limits_{i=1}^{m'}n'(m'-i)[1+2+3+…+n'-1]](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-3185ee9777553ecaf2737047e03f4dc8_l3.png)
![Rendered by QuickLaTeX.com =\sum\limits_{i=1}^{m'}n'(m'-i)[(1+n'-1)(n'-1)/2]](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-b7d9c10aef39512b200b776fe52bf592_l3.png)
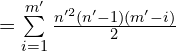
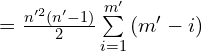
![]()
![]()
![]()
再化简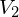 :
:
![Rendered by QuickLaTeX.com \begin{aligned}V_2&= \sum\limits_{i=1}^{m'} \sum\limits_{j=1}^{n'}(n'-1)(m'-i)^2 \&= \sum\limits_{i=1}^{m'} n'(n'-1)(m'-i)^2 \&=n'(n'-1) \sum\limits_{i=1}^{m'}(m'-i)^2 \&=n'(n'-1)[0^2+1^2+2^2+…+(m'-1)^2]\end{aligned}](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-31286fcfa0ed35f27424baded8b32de1_l3.png)
根据平方和的求和公式:![]() ,有
,有
![]()
最后化简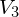 :
:
![]()
![Rendered by QuickLaTeX.com = \sum\limits_{i=1}^{m'} \sum\limits_{j=1}^{n'} \frac{1}{2}(m'-i)(n'-1)[(m'-i)(n'-1)-1]](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-c9dbd84d35fdd4a00b5dd97c9354db14_l3.png)
![Rendered by QuickLaTeX.com =\frac{n'}{2}\sum\limits_{i=1}^{m'}(m'-i)(n'-1)[(m'-i)(n'-1)-1]](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-bbd0f93bdc9f03a3bbd24022b524704d_l3.png)
![Rendered by QuickLaTeX.com =\frac{n'}{2}\sum\limits_{i=1}^{m'}[(m'-i)^2(n'-1)^2-(m'-i)(n'-1)]](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-f9acdeb08d1557904188ca7bdb315522_l3.png)
![Rendered by QuickLaTeX.com =\frac{n'}{2}[(n'-1)^2\sum\limits_{i=1}^{m'}(m'-i)^2 -(n'-1)\sum\limits_{i=1}^{m'} (m'-i) ]](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-0f00401b44a44f7eda6d7c556d04d08e_l3.png)
![]()
同样地,由平方和求和公式和等差数列求和公式:
![]()
最后,我们就可以![]() 计算出
计算出![]() 了(注意最后一行是加号不是等号):
了(注意最后一行是加号不是等号):
![]()
然后其实已经没有必要再化简了。
好,无论以哪种方法,我们已经计算出来![]() 了。
了。
接下来计算![]() 。
。
计算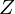 :
:
计算![]() 是一件很麻烦的事情。我们可以计算出每条非水平非直线上的点数。如果这个点数为
是一件很麻烦的事情。我们可以计算出每条非水平非直线上的点数。如果这个点数为![]() ,那么在这条斜线上共线的方案数就是
,那么在这条斜线上共线的方案数就是![]() 现在的问题是,如何计算每条直线的
现在的问题是,如何计算每条直线的![]() 。
。
为了方便叙述,我们还是设![]() 。所以共有
。所以共有![]() 个点可以作为三角形的顶点。同时,我们先算左上—右下方向的斜线对答案的贡献。由对称性可知,右上—左下方向的斜线对答案的贡献和它是相同的。
个点可以作为三角形的顶点。同时,我们先算左上—右下方向的斜线对答案的贡献。由对称性可知,右上—左下方向的斜线对答案的贡献和它是相同的。
引理
平面直角坐标系上的点![]() 与
与![]() 连线上的整数点共有
连线上的整数点共有![]() 个。(
个。(![]() )
)
证明(参考了这里)
设![]() 。
。
已知![]() 连线上的点
连线上的点![]() 必定满足
必定满足![]()
即![]()
由![]() 的最大性可知,
的最大性可知,![]()
(假设![]() ,那么
,那么![]() ,
,![]() ,显然
,显然![]() 会有更大的公约数
会有更大的公约数![]() ,而不是
,而不是![]() 。产生矛盾,所以假设不成立)
。产生矛盾,所以假设不成立)
意即,![]() 互质,
互质,![]() ,所以
,所以![]() 不为整数。
不为整数。
要使得![]() 为整数,首先要满足
为整数,首先要满足![]() 为
为![]() 内的整数,并且
内的整数,并且![]() 。所以
。所以![]() 必须为
必须为![]() 的整数倍。又因为
的整数倍。又因为![]() ,所以
,所以![]() 内有
内有![]() 个整数
个整数![]() ,满足
,满足![]() 。(这
。(这![]() 个整数
个整数![]() 分别是
分别是![]() ,可以写成
,可以写成![]() 的形式)。
的形式)。
证毕。
从上面的引理可知,若以![]() 为右下端点:以
为右下端点:以![]() 为左上端点的线段上有
为左上端点的线段上有![]() 个整点,以
个整点,以![]() 为左上端点的线段上有
为左上端点的线段上有![]() 个整点,…,以
个整点,…,以![]() 为左上端点的线段上有
为左上端点的线段上有![]() 个端点。
个端点。
我们设![]() 表示大小为
表示大小为![]() 的点阵里,有多少组三点共线且包含了左上角
的点阵里,有多少组三点共线且包含了左上角![]() 。为什么要这么算呢?因为只要能算出来
。为什么要这么算呢?因为只要能算出来![]() 大小的点阵包含了左上角的的三点共线组数,我们就能算出来包含了右下角、左下角、右上角的——由于对称性,它们的答案是一样的。
大小的点阵包含了左上角的的三点共线组数,我们就能算出来包含了右下角、左下角、右上角的——由于对称性,它们的答案是一样的。
已知当前计算的三点包含了左上角[ 假设是![]() 而不是
而不是![]() ] 。左上—右下走向的共线的三点里一定有一个在最右下方。我们以最右下方的这个点为分类标准,依次统计。这样就能不重不漏。
] 。左上—右下走向的共线的三点里一定有一个在最右下方。我们以最右下方的这个点为分类标准,依次统计。这样就能不重不漏。
那么,确定了最左上方和最右下方的点,与这两个点构成三点共线的组数就可以由中间那个点唯一确定了。
若最右下方的点坐标为![]() ,它和
,它和![]() 之间有
之间有![]() 个整点可以做“三点共线”中的第三点。因此以
个整点可以做“三点共线”中的第三点。因此以![]() 为右下端点,对统计的贡献就是
为右下端点,对统计的贡献就是![]()
因此有递推公式:![]()
上面仅仅统计了包含![]() 这个点的左上—右下走向共线的三点数。如何由此得到整个问题的答案?
这个点的左上—右下走向共线的三点数。如何由此得到整个问题的答案?
由对称性我们可以知道,![]() 还表示大小为
还表示大小为![]() 的点阵中,以
的点阵中,以![]() 为最右下点的左上—右下走向的共线的三点数。如果有左上—右下走向的三点,它们最右下的点不同,说明这三点是不可能相同的。
为最右下点的左上—右下走向的共线的三点数。如果有左上—右下走向的三点,它们最右下的点不同,说明这三点是不可能相同的。
也就是说,![]() 的点阵中,所有左上—右下走向的三点共线方案数为
的点阵中,所有左上—右下走向的三点共线方案数为![]() ,其中
,其中![]()
最后做一个前缀和![Rendered by QuickLaTeX.com s[x][y]=\sum\limits_{i=1}^x\sum\limits_{j=1}^{y}f[i][j].](https://blog.hzao.top/wp-content/ql-cache/quicklatex.com-26e6a3d13bca8eb387a01a1e959c8baf_l3.png)
终于可以得到![]()
然后回顾之前的内容,整个问题就解决了。
代码实现应该算简单,我就不放了。