题解 P1494 【[国家集训队]小Z的袜子】

发布者：Hzao 于题解 P1494 【[国家集训队]小Z的袜子】留下评论

看了一下题解里的大佬，好像都用的莫队或者分块维护平方和…

其实用不着维护平方和。

从头开始说吧。

求什么

对于每个询问q（q包含q.l,q.r），我们要求出任取两个袜子颜色相同的概率。假设在区间[l,r]取到颜色为i的袜子的概率为P(l,r,i)，那么要求的就是\sum_{i=1} ^{n} P(q.l,q.r,i)。

怎么求

那么对于任意的L,R,i,如何计算P(L,R,i)？假设在[L,R]内i袜子的个数为n_i，根据数学知识，要取到两只i，首先要取第一只i颜色的袜子。因为有n_i只袜子都是i颜色的，所以取第一只i袜子的方案数为n_i。然后再取第二只i颜色的袜子。由于已经取了1只i颜色的袜子，就只剩下i-1只可选了。这样的排列数有n*(n-1)个。

计算概率时有顺序用排列，无顺序用组合，因为我们只关心两只袜子是否颜色相同，所以这道题中选袜子的顺序是没有影响的。而刚刚计算的只是排列数，每种组合方式被计算了2次（选第1,3只白袜和选第3,1只白袜是一样的）。所以要除以2。
即选到两只i颜色的袜子的方案数n_i(n_i-1)/2.

在[L,R]内，有R-L+1只袜子，在这其中选择两只，方案总数为C_{R-L+1}^2。（都在刷国家集训队的题目了，你应该知道组合数吧…. ）

所以P(L,R,i)=n_i*(n_i-1)/2 C_{R-L+1}^2 .

答案如前所述，为\sum_{i=1} ^{n} P(q.l,q.r,i)

怎么优化

1.分块。

如果直接对每个询问区间暴力维护n_i，O(m* k n)级别的复杂度很显然过不了。（k是一个常数。其实我不太会分析复杂度所以欢迎dalao指正）

以样例为例，(话说这个样例不会被敏感词拦截吗)

6 4

1 2 3 3 3 2

2 6

1 3

3 5

1 6

样例图解

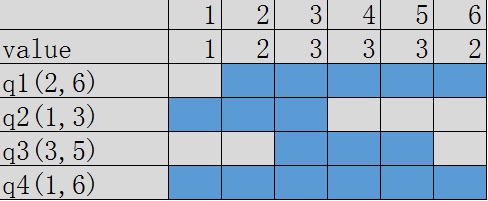
我们发现一些询问都和其它某（几）个询问有重叠部分。那其实，我们可以把有重叠部分的询问分组，先处理每组的第一个询问，然后处理与上一个询问不同的部分。

于是我们可以先按照左端点的大小排序，然后把排序后的队列分成几个小块（一般大小取\sqrt{m}）。然后再在每个块内以右端点大小排序。我们就可以以块为单位处理。

虽然左端点的单调性在第二次排序的时候打乱了，但是第一次排序保证了同一个块内相邻两个左端点的变化在\sqrt{n}内。第二排序可以保证右端点只有加操作，没有减操作。

2.统计

前面有些大佬提到了维护平方和的办法。但是其实我认为有更好的办法（每次修改三行代码变为一行）。
进入每一个块内处理的时候，我们先暴力求出第一组询问的区间内，每个袜子的个数，存在数组num里。然后在前一个询问的基础上，对num修改。
根据前面的推导，对每个询问q,我们要求的是

\sum_{i=1}^{n}P(q.l,q.r,i)=num_i*(num_i-1)/2 C_{q.r-q.l+1}^2 .

(C右上角的2不是平方的意思…)

可以看出，同一个询问的分母都是确定的。所以我们现在关心如何通过修改num来快速得到分子。

重点来了，假设原来的num_i=x。

假如我们要对num_i执行增加1的操作，那么实际上跟i有关的那一部分的分子的变化为：
增加后-增加前=(x+1)x-x(x-1)=2x.所以我们直接加上原来x的两倍即可。

假如我们要对num_i执行减小1的操作，那么实际上i这一部分分子的变化为：

减少后-减少前= (x-1)(x-2)-x(x-1)=-2(x-1)，所以我们直接减去减少后的num_i的两倍即可。

于是以前的更改代码为：（以增加为例）

{

    tot-=num[i]* num[i];
    num[i]++;
    tot+=num[i]* num[i]; 
}

现在只需要：

{
    tot+=2* num[i]++;
}

但是….分母不是还有一个2么，直接约分不就行了…

于是乘以2可以直接省略，得到：

{
    tot+=num[i]++;
}

不开O2 363ms

开O2 191ms

细节见代码：

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using std::sort;
const int maxn=50000;
struct que
{
    int l,r,id;
}q[maxn+5];
struct blk
{
    int l,r;
}b[333];
int col[maxn+5],num[maxn+5],ans1[maxn+5],ans2[maxn+5],c[maxn+5][3];
//依次保存 颜色，上文中的num数组，分子，分母，组合数
int n,m,bs,bn,tot;
//bs为每个块的大小 bn为块的个数
//排序后可以一边分块一边计算
inline void read(int &x){//快读
    x=0;
    char c;
    do{
        c=getchar();
    }
    while(c<'0'||c>'9');
    do{
        x=x*10+c-'0';
        c=getchar();
    }
    while(c>='0'&&c<='9');
}
inline int min(int a,int b){
    return a<b?a:b;
}
inline int gcd(int a,int b){
    return b?gcd(b,a%b):a;
}
inline bool cmpl(que a,que b){//以l排序
    return a.l<b.l;
}
inline bool cmpr(que a,que b){//以r排序
    return a.r<b.r;
}
inline void pre(){//计算组合数
    c[1][0]=c[1][1]=1;
    for(register int i=2,j;i<=n;++i){
        c[i][0]=1;
        for(j=1;j<=2;++j){
            c[i][j]=c[i-1][j-1]+c[i-1][j];
        }
    }
}
int main(){
    read(n);
    read(m);
    pre();
    for(register int i=1;i<=n;++i){
        read(col[i]);
    }
    for(register int i=1;i<=m;++i){
        read(q[i].l);
        read(q[i].r);
        q[i].id=i;
    }
    bs=sqrt(m);
    sort(q+1,q+1+m,cmpl);
    //整体按l排序，保证每个块内左端点的变化不会太大
    for(register int i=1,g;i<=m;i+=bs){
    //i为每个块的左边界
        b[++bn].l=i;
        b[bn].r=min(i+bs-1,m);
        sort(q+i,q+b[bn].r+1,cmpr);//块内按右端点排序 以免右边反复无用增减                    
        memset(num,0,sizeof(num));
        tot=0;//分子
        //先处理这个块里的第一个询问
        for(register int j=q[b[bn].l].l;j<=q[b[bn].l].r;++j){
            tot+=num[col[j]]++;
        }
        ans1[q[b[bn].l].id]=tot;
        ans2[q[b[bn].l].id]=c[q[b[bn].l].r-q[b[bn].l].l+1][2];
        //分母无需再乘以二，因为分子计算的时候省略了二
        if(ans1[q[b[bn].l].id]==0)ans2[q[b[bn].l].id]=1;
        else {
                g=gcd(tot,ans2[q[b[bn].l].id]);
                ans1[q[b[bn].l].id]/=g;
                ans2[q[b[bn].l].id]/=g;
         }

         //在前面的基础上，处理块内其他询问
        for(register int k,j=b[bn].l+1;j<=b[bn].r;++j){
             if(q[j-1].l<q[j].l){//处理这一次询问少了的部分（复原）
                 for(k=q[j-1].l;k<q[j].l;++k){
                    tot-=--num[col[k]];
                    //注意运算符在前（根据推导，这里使用减少后的值）
                 }
             }
             else {
                for(k=q[j].l;k<q[j-1].l;++k){//处理这一次询问多出来的部分
                    tot+=num[col[k]]++;
                    //注意运算符在后（根据推导，这里使用增加前的值）
                }
             }

             for(k=q[j-1].r+1;k<=q[j].r;++k){//处理这个询问后面多出来的部分
                tot+=num[col[k]]++;
             }
             ans1[q[j].id]=tot;
             ans2[q[j].id]=c[q[j].r-q[j].l+1][2];
             if(ans1[q[j].id]==0)ans2[q[j].id]=1;
             else {
                g=gcd(tot,ans2[q[j].id]);
                ans1[q[j].id]/=g;
                ans2[q[j].id]/=g;
             }
        }
    }
    for(register int i=1;i<=m;++i){
        printf("%d/%d\n",ans1[i],ans2[i]);
    }
    // system("pause");
    return 0;
}

祝AC..

留下评论

您的电子邮箱地址不会被公开。 必填项已用 * 标注