题解 UVA1073 【Glenbow Museum】

如果有一个点能看到各个顶点，那么这个点的上下左右一定要对应四个。

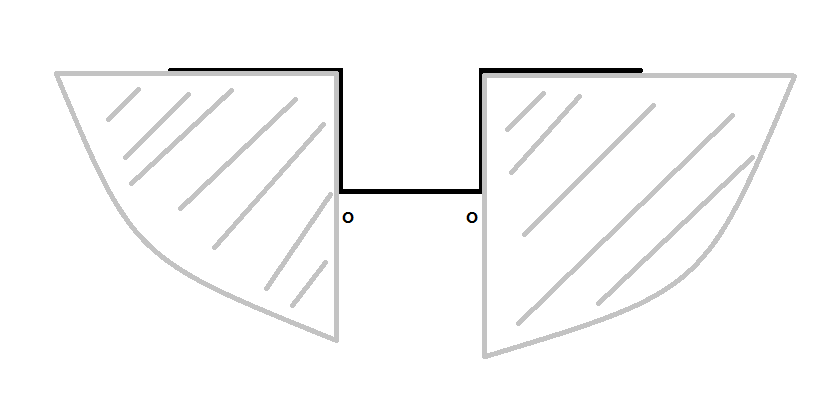
如果有，那么这两个°的角延伸出去的角的可视范围没有交集，即它们不能被同时被看到（点能看到点，那么点也能看到点。反之一定不能看到点），如下图所示：（延伸出去的角可能是也可能是，这里以为例）

所以一定不能有。

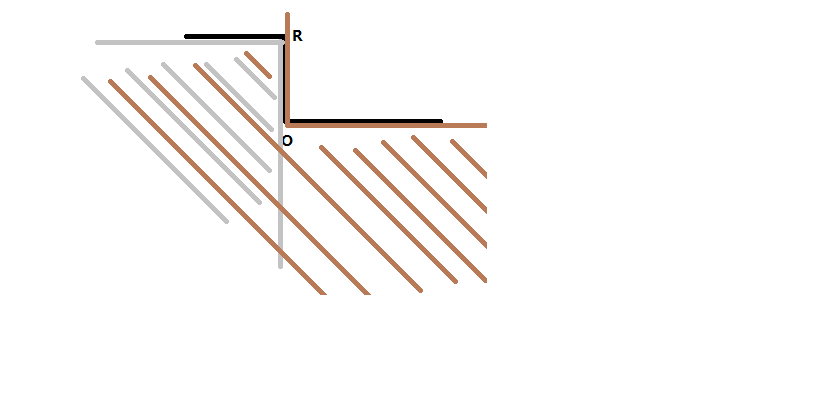
如果没有，但是有。那么前面一个字符一定是。（否则就有了）。这两个角的可视范围是有交集的。如下图所示：

同样地，相邻的两角的可视范围也是有交集的。至少它们两个角是可以被同时看到的。

如果一个点能看到所有内角，那么它的正对的上下左右一定都是。因为如果某个方向是，显然成立。如果某个方向上的角度序列有，那么这个方向的角度序列只能是。即只能以结尾。（如果一直不结尾，那就不构成多边形。如果以结尾，那么不合法）。

既然以结尾，那么能同时看到这个的点一定在如图所示的灰色区域。

反过来说，一个点的正对的上下左右四个方向一定是。

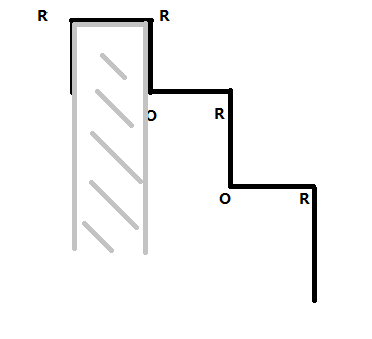
稍加思考可以发现，只要满足上下左右四个方法有，且整个序列没有，那么一定满足条件。(没有意味着不会往外拐)

个内角代表条边，根据多边形内角和公式：

又因为

所以有

所以我们要求的就是个和个的字符串中，有至少四个且没有的个数。注意或者为奇数时无解。（为奇数时的内角和不为°的整数倍）

前两个实现方法参考《算法竞赛入门经典：训练指南》:

方法一：

用表示有个，个，开头为（表示，表示），结尾为。

则

且

（不能出现）

答案就很显然了（把几个加起来），你可以自行推一推或者见代码。

递归加上记忆化即可解决。（直接递推则需）

代码：

#include<cstdio>
#include<cstring>
int L,kase;
long long d[520][520][2][2];
long long f(int i,int j,int b,int e){
    if(~d[i][j][b][e]){
        return d[i][j][b][e];
    }
    if(!j){
        return i&&!b&&!e;
    }
    if(!i){
        return j==1&&b==1&&e==1;
    }
    if(e){
        return d[i][j][b][e]=f(i,j-1,b,0);
    }
    else{
        return d[i][j][b][e]=f(i-1,j,b,0)+f(i-1,j,b,1);
    }
}
int main(){
    memset(d,-1,sizeof(d));
    long long ans;
    while(~scanf("%d",&L)&&L){
        ans=0;
        if(!(L&1||L<4)){
            ans+=f((L+4)/2,(L-4)/2,0,0);
            ans+=f((L+4)/2,(L-4)/2,1,0);
            ans+=f((L+4)/2,(L-4)/2,0,1);
        }
        printf("Case %d: %lld\n",++kase,ans);
    }
    return 0;
}

方法二：

表示以开头，有个，有对相邻的（算两对，算对），且以结尾的方案数。

则

其余.表示当前字符串可由某个结尾的字符加上或来得到。

设。

答案是

第一项表示开头结尾。

第二项表示开头结尾。求的是字符串中只有对。但是把开头和结尾这一对算上就有对了。

第三项很难理解，它表示开头结尾。每一个开头结尾的合法字符串都对应一个把最后一个去掉之后的，开头结尾的字符串。因为最后一个字符是，不能和前面的接在一起，所以需要保证前面就有个。

也就是说把个对的开头结尾的字符串后面加上一个就可以得到个对的开头结尾的字符串。

代码：

#include<cstdio>
#include<cstring>
int L,kase;
long long d[520][520][2];
long long f(int i,int j,int k){
    if(i==1){
        return !j;
    }
    if(~d[i][j][k])return d[i][j][k];
    return d[i][j][k]=f(i-1,j,k)+f(i-1,j-1,k);
}
int main(){
    memset(d,-1,sizeof(d));
    while(~scanf("%d",&L)&&L){
        if(L&1||L<4){
            printf("Case %d: 0\n",++kase);
            continue;
        }
        printf("Case %d: %lld\n",++kase,
            f((L+4)/2,3,0)+//R...R
            f((L+4)/2,4,1)+//O...R
            f((L+4)/2,4,0)  //R...O
        );
    }
    return 0;
}

方法三：（参考了KobeDuu的博客）

组合计数。

其实可以发现，只要有个，个(其实)，并且不相连，那么一定可以保证有4个对。

可以这样想：把个连成一个环，那么有个对。

再把个插入，每插入一个，就会少一个对。

所以最后剩下个对。刚好满足条件。

所以可以这样利用组合数算,把所有排成一行之后：

在开头放

那么，最后一个位置不能放。剩下个位置可以放，要放下个。

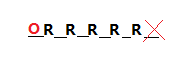
计数

不在开头放

那么剩下个位置可以放个。
计数

所以答案为

代码太简单就略了吧。

祝AC。