自己搞出来一种树状数组+倍增的做法,A掉之后发现网上的题解都是平衡树。心里还是有点美滋滋。
于是决定分享出来。(其实只是想找个借口颓废一下)
不过其实非常简单,耐心读一读就懂了。
在阅读实现部分之前,请不要考虑“这个操作怎么实现呢?”“时间复杂度会不会过高?”这类的问题。否则很可能你会很快放弃阅读。先理解这种做法的流程即可。(可以先剧透一下:时间复杂度大约是![]() )
)
题意分析
分析一下题意,其实就是给定一棵树,在这棵树上选择某几个节点(设这几个节点的集合为![]() ),求从其中的某个节点出发,经过所有被选择的节点后再回到出发点的最短路径长度。
),求从其中的某个节点出发,经过所有被选择的节点后再回到出发点的最短路径长度。
从起点到终点,和从终点到起点的路径长度![]() 是一样的,仅仅是沿原路返回而已。
是一样的,仅仅是沿原路返回而已。
也就是说,我们要求的即是将所有![]() 中的节点连接起来的路径长度的二倍,即
中的节点连接起来的路径长度的二倍,即![]() 。
。
下两图分别是![]() 时的路径和
时的路径和![]() 时的路径,请自行理解,我就不再赘述。
时的路径,请自行理解,我就不再赘述。
(在机房只能用Windows 7的画图工具,只能说还算能看吧)
.png)
.png)
那么,我们可以求出把选择的所有节点连接起来的最短路径,然后输出它的二倍。
于是题目就变成了,动态维护使树上某些节点连通的最短路径长度,并且在每一次修改操作完成后输出这个长度的二倍。
解决方案
题目中有两种操作,增加选择的节点和删除选择的节点。
假设要处理的节点为![]() ,我们先考虑将向
,我们先考虑将向![]() 中增加
中增加![]() 的情况。删除
的情况。删除![]() 的情况是可以建立在增加
的情况是可以建立在增加![]() 的情况之上的:令
的情况之上的:令![]() ,在
,在![]() 中删除
中删除![]() 的花费就是在
的花费就是在![]() 中增加
中增加![]() 的花费——他们是前后两种路径长度的差。
的花费——他们是前后两种路径长度的差。
现在考虑增加![]() 时的情况。
时的情况。
情况1.![]() ,即
,即![]() 中还没有任何节点。向其中加入
中还没有任何节点。向其中加入![]() 也不会产生任何长度。因此可以不修改答案。
也不会产生任何长度。因此可以不修改答案。
情况2.在原图中,![]() 至少有两个子节点(设其中一个为
至少有两个子节点(设其中一个为![]() ) ,满足以
) ,满足以![]() 为根节点的子树中有节点属于
为根节点的子树中有节点属于![]() 。
。
于是![]() 是属于
是属于![]() 的2个(或更多)点的
的2个(或更多)点的![]() ,使他们连通则必须经过
,使他们连通则必须经过![]() 。那么,在加入
。那么,在加入![]() 之前,使节点连通的路径就已经经过了
之前,使节点连通的路径就已经经过了![]() ,因此可以不修改答案。
,因此可以不修改答案。
如下图所示,![]() 的两个子节点
的两个子节点![]() 的子树中都至少有一个节点在
的子树中都至少有一个节点在![]() 中,在加入
中,在加入![]() 之前,连通
之前,连通![]() 中节点的路径就已经经过了
中节点的路径就已经经过了![]() 。即加入
。即加入![]() 也不会对答案造成影响。
也不会对答案造成影响。
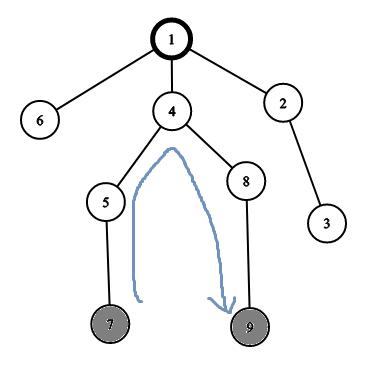
情况3.在原图中,以![]() 为根的子树中有节点属于
为根的子树中有节点属于![]() ,并且以
,并且以![]() 为根的子树外也有节点属于
为根的子树外也有节点属于![]() 。
。
那么同上,在加入![]() 之前,使节点连通的路径已经经过了
之前,使节点连通的路径已经经过了![]() 。换句话说,
。换句话说,![]() 的加入不会对路径长度造成影响,因此不需要修改答案。
的加入不会对路径长度造成影响,因此不需要修改答案。
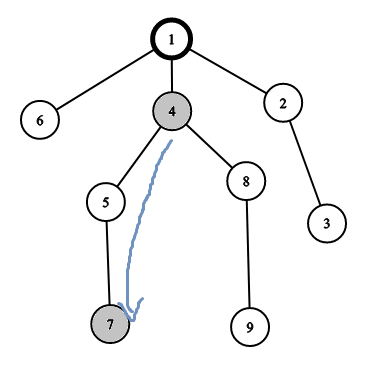
如图所示,假如要加入![]() ,在加入
,在加入![]() 之前已有
之前已有![]() ,连接
,连接![]() 的路已经覆盖了
的路已经覆盖了![]() ,因此加入
,因此加入![]() 不会使答案改变。
不会使答案改变。
情况4.不满足上述三种情况中的任何一个。
那么我们需要找到一个在原路径上的点![]() ,满足
,满足![]() 最小。并且使答案加上
最小。并且使答案加上![]() 。
。
寻找![]() 的方法是,从
的方法是,从![]() 开始向上倍增,找到离
开始向上倍增,找到离![]() 最近的,且子树中有节点属于
最近的,且子树中有节点属于![]() 的点。设这个点为
的点。设这个点为![]() 。
。
那么:
![]() 假如
假如![]() 在原有路径上,即加入
在原有路径上,即加入![]() 之前,
之前,![]() 就被使节点连通的路径覆盖。也就是说,
就被使节点连通的路径覆盖。也就是说,![]() 满足情况2或情况3。
满足情况2或情况3。
此时![]() 。
。
那么只需要让答案加上![]()
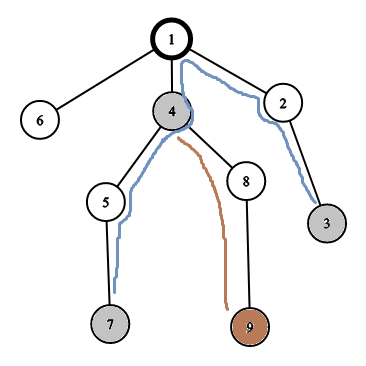
即,如下图所示:
![]() ,
,![]() 是
是![]() 能到达的 最近的 子树中有节点在
能到达的 最近的 子树中有节点在![]() 中的 点。
中的 点。
那么只需要将![]() 与
与![]() 连接起来即可。
连接起来即可。
![]() 假如
假如![]() 不在原有路径上,那么以
不在原有路径上,那么以![]() 的子树外一定没有节点在
的子树外一定没有节点在![]() 中。(否则满足情况3,原有路径一定经过
中。(否则满足情况3,原有路径一定经过![]() )
)
也就是说,![]() 中的点全部都在以
中的点全部都在以![]() 为根的子树中。
为根的子树中。
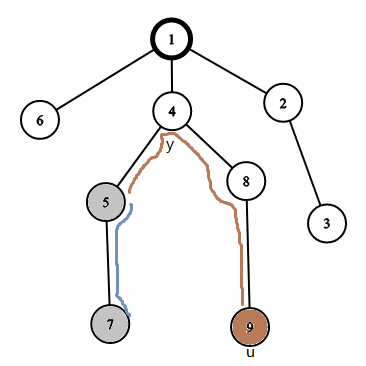
我们只需要在这当中选择一个离![]() 最近的点,将它与
最近的点,将它与![]() 连起来即可。
连起来即可。
如下图所示:
那如何寻找离![]() 最近的
最近的![]() 呢?(请先往上翻,确认自己已知悉
呢?(请先往上翻,确认自己已知悉![]() 的含义后再继续阅读)
的含义后再继续阅读)
由![]() 可知,无论选择哪个点,都有一段
可知,无论选择哪个点,都有一段![]() ,而这段距离是已固定的。(当前只有
,而这段距离是已固定的。(当前只有![]() 不确定)
不确定)
所以我们要找的其实是![]() 最小的点。
最小的点。
由于![]() 是
是![]() 的父节点,所以有:
的父节点,所以有:
![]()
而![]() 是恒定的。
是恒定的。
所以我们要找的就是![]() 最小的点。
最小的点。
于是可以先处理出每个点到根节点(任选一个即可)的距离。
以上的讨论就包含所有的情况了。
代码实现
上述流程有几个需要高效算法维护的内容:
1.节点![]() 的子树中有多少节点属于
的子树中有多少节点属于![]() ;
;
2.离节点![]() 最近的 子树中有节点属于
最近的 子树中有节点属于![]() 的 点;
的 点;
3.树上任意两点间的距离;
4.已经被路径覆盖的点中,距离根最近的点。
由于要维护子树中的信息,很自然地想到用![]() 序。设
序。设![]() 表示深度优先搜索时,
表示深度优先搜索时,![]() 是第几个被遍历到的。
是第几个被遍历到的。![]() 表示从
表示从![]() 往上回溯时,已经遍历了多少的点。
往上回溯时,已经遍历了多少的点。
则![]() 的子树中的点就是
的子树中的点就是![]() 序在
序在![]() 中间的点。
中间的点。
当我们要将![]() 加入到
加入到![]() 中时,令
中时,令![]() 。那么
。那么![]() 就是以
就是以![]() 为根的子树中在
为根的子树中在![]() 中的个数。
中的个数。
用树状数组维护即可。
于是1就解决了。单次操作![]() 。
。
树上![]() 之间的距离等于
之间的距离等于![]() ,于是用
,于是用![]() 维护即可。巧了,我们本来就要维护每个节点的
维护即可。巧了,我们本来就要维护每个节点的![]() 啊,一举两得。
啊,一举两得。
于是问题3解决。单次操作![]() 。
。
由于只要![]() 的子树中有节点属于
的子树中有节点属于![]() ,那么
,那么![]() 的父节点(或者父节点的父节点,等等)中也一定有节点属于
的父节点(或者父节点的父节点,等等)中也一定有节点属于![]() 。换句话说,”子树中是否有节点属于
。换句话说,”子树中是否有节点属于![]() “ 这一属性具有单调性。
“ 这一属性具有单调性。
于是可以用倍增的方法。每次向上倍增某个节点的![]() 个祖先,找到最近的即可。
个祖先,找到最近的即可。
(又巧了,倍增![]() 不正好维护了每个节点的
不正好维护了每个节点的![]() 倍祖先么?)
倍祖先么?)
于是问题2可在![]() 内解决。
内解决。
最巧的是问题4。 由于树的形态确定后,每个点![]() 的
的![]() 都是不变的,所以可以考虑小根堆维护。
都是不变的,所以可以考虑小根堆维护。
但是,是不是我们要把路径上所有的点(包括没在![]() 中的点)都加入小根堆?如果是,那么每次需要
中的点)都加入小根堆?如果是,那么每次需要![]() 的时间来找出路径上的点并将其加入小根堆中。这显然是不可接受的。
的时间来找出路径上的点并将其加入小根堆中。这显然是不可接受的。
重新考虑之前讨论的4种加入点的情况。除了在![]() 中的点,我们只需要将距离根最近的点加入小根堆即可。
中的点,我们只需要将距离根最近的点加入小根堆即可。
例如,在情况1(![]() )中,我们将这唯一添加进去的点加入小根堆即可。
)中,我们将这唯一添加进去的点加入小根堆即可。
在情况2(有至少两个子树中有点属于![]() )中,我们将正在处理的
)中,我们将正在处理的![]() (即图中的
(即图中的![]() )加入小根堆即可。它就是最近的,最有可能被选中的点。
)加入小根堆即可。它就是最近的,最有可能被选中的点。

假如![]() 在后面被删掉了怎么办?会不会遗漏
在后面被删掉了怎么办?会不会遗漏![]() 这种候选项?
这种候选项?
不会。
假如![]() 被删掉,我们先不在小根堆中删除
被删掉,我们先不在小根堆中删除![]() ,而是在取用它的时候判断它是否在路径上。只要它在路径上(满足情况2或3或者本身就是
,而是在取用它的时候判断它是否在路径上。只要它在路径上(满足情况2或3或者本身就是![]() 中的点),就直接取用,否则将它弹出,考虑下一个候选项。
中的点),就直接取用,否则将它弹出,考虑下一个候选项。
如果![]() 被弹出,那么除非有其它操作使得
被弹出,那么除非有其它操作使得![]() 或
或![]() 在路径上,否则候选项肯定不可能是
在路径上,否则候选项肯定不可能是![]() 或
或![]() 。
。
而当其它操作使得![]() 或
或![]() 在路径上并且可能成为备选点时,我们会将
在路径上并且可能成为备选点时,我们会将![]() 或
或![]() 加入小根堆,所以不会遗漏。
加入小根堆,所以不会遗漏。
类似地,在情况3下,将要处理的点(图中的9)加入小根堆即可。

在情况4下,将倍增找到的点和正处理的点加入小根堆即可。
其实我们发现,除了要向上倍增的情况,所有情况都要将要处理的点加入小根堆中。
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
//#define LOC
#define nowy (L[i].to)
using std::queue;
using std::priority_queue;
template <typename T>
inline void read(T &x){
x=0;char c; T f=1;
do{c=getchar();if(c=='-')f=-1;}while(c>'9'||c<'0');
do{x=x*10+c-'0';c=getchar();}while(c>='0'&&c<='9');x*=f;
}
const int N=1e5 + 10;
int n,m,t;
int h[N],tot=1;
int f[N][18];
int d[N];
long long len[N];
int bg[N],ed[N];
int Inq[N];
int DFN;
int TotIn;
int Diff[N];//Diff是FT的一个拷贝 便于直接确认一个点是否在S中
int x,y,z;
int Num_SonIn,Cls_F;
long long ans=0;
struct line{
int to,nxt,w;
}L[2*N];
struct OneNode{
int num;
bool operator <(const OneNode b)const {
if(len[num]==len[b.num])return d[num]>d[b.num];
return len[num]>len[b.num];
}
OneNode(int x):num(x){}
};//通过便于维护小根堆
struct FenwickTree{
int v[N];
inline void clear(){
memset(v,0,sizeof(v));
}
inline void add(int x,int y){
for(;x<=n;x+=x&-x){
v[x]+=y;
}
}
inline int ask(int x){
int res=0;
while(x>0){
res+=v[x];
x-=x&-x;
}
return res;
}
FenwickTree(){clear();}
}FT;
priority_queue<OneNode> OQ;
inline void add(int x,int y,int z){
L[++tot].to=y;L[tot].nxt=h[x];h[x]=tot;L[tot].w=z;
L[++tot].to=x;L[tot].nxt=h[y];h[y]=tot;L[tot].w=z;
}
void GetLCA_DFS(int x){
//DFS 同时求出祖先数组、距离根节点的距离、DFS序
bg[x]=++DFN;
for(int i=h[x];i;i=L[i].nxt){
if(d[nowy])continue;
d[nowy]=d[x]+1;
f[nowy][0]=x;
len[nowy]=len[x]+L[i].w;
for(int j=1;j<=t;++j){
f[nowy][j]=f[f[nowy][j-1]][j-1];
}
GetLCA_DFS(nowy);
}
ed[x]=DFN;
}
inline int LCA(int x,int y){
if(d[x]>d[y]){
x^=y;y^=x;x^=y;
}
//d[x]<=d[y]
for(register int i=t;i>=0;--i){
if(d[f[y][i]]>=d[x]){
y=f[y][i];
}
}
if(x==y)return x;
for(register int i=t;i>=0;--i){
if(f[y][i]!=f[x][i]){
y=f[y][i];
x=f[x][i];
}
}
return f[x][0];
}
inline long long LEN(int x,int y){
return 1ll*len[x]+len[y]-2*len[LCA(x,y)];
}
inline int GetSonIn(int x){//including x
//判断x的子树中有多少节点属于S
if(!x)return TotIn;
int Num=FT.ask(ed[x])-FT.ask(bg[x]-1);
return Num;
}
inline bool TwoSon(int x,int v){
//是否满足情况2
int SonV;
for(register int i=h[x];i;i=L[i].nxt){
if(d[nowy]<=d[x])continue;
SonV=GetSonIn(nowy);
if(SonV){
if(SonV==v)return false;
return true;
}
}
return false;
}
inline bool check(int x){
//是否满足情况2或3 这两种情况可以一同处理
if(!x)return true;
int Num_SonIn;
return (Num_SonIn=GetSonIn(x))&&(Num_SonIn<TotIn||TwoSon(x,Num_SonIn));
}
inline int GetCls_F(int x){
//倍增求离自己最近的 子树里有节点属于S 的节点
if(GetSonIn(x))return x;
int Num;
for(register int i=t;i>=0;--i){
if(!(Num=GetSonIn(f[x][i]))){
x=f[x][i];
}
}
return f[x][0];
}
inline void Change(long long t){
//通过t变量实现增加删除在同一个函数处理 减少码量
if(TotIn!=0){
if(!check(x)){
Cls_F=GetCls_F(x);
if(check(Cls_F)){
if(t&&!Inq[Cls_F]){OQ.push(OneNode(Cls_F));Inq[Cls_F]=1;}
ans+=LEN(x,Cls_F)*(-1+2*t);
}
else {
while(!OQ.empty()){
z=OQ.top().num;
if(check(z)||Diff[z])break;
OQ.pop();
Inq[z]=0;
}
if(t&&!Inq[Cls_F]){OQ.push(OneNode(Cls_F));Inq[Cls_F]=1;}
ans+=LEN(x,z)*(-1+2*t);
}
}
}
}
int main(){
read(n);read(m);
t=log(n)/log(2)+1;
for(register int i=1;i<n;++i){
read(x);
read(y);
read(z);
add(x,y,z);
}
d[1]=1;
GetLCA_DFS(1);
for(register int i=1;i<=m;++i){
read(x);
if(!Diff[x]){
Change(1);
FT.add(bg[x],1);
Diff[x]+=1;
if(!Inq[x]){Inq[x]=1;OQ.push(OneNode(x));}
++TotIn;
}
else{
--TotIn;
FT.add(bg[x],-1);
Diff[x]-=1;
Change(0);
}
printf("%lld\n",ans*2);
}
return 0;
}然后就可以愉快地AC了。
Uae牛逼!